«Το Θεώρημα των τεσσάρων χρωμάτων» world!

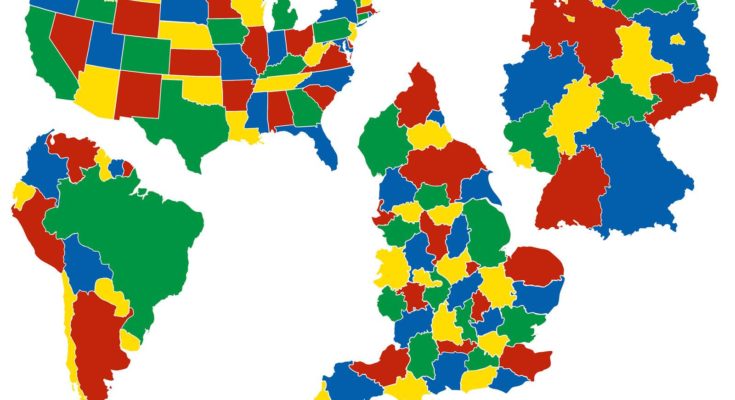
Στα μαθηματικά το Θεώρημα των τεσσάρων χρωμάτων, ή το Θεώρημα των χαρτών των τεσσάρων χρωμάτων δηλώνει ότι, δεδομένου του διαχωρισμού ενός επιπέδου σε γειτονικές περιοχές, παράγοντας έτσι ένα χάρτη, δεν απαιτούνται περισσότερα από τέσσερα χρώματα για να χρωματιστούν οι περιοχές του χάρτη, έτσι ώστε να μην υπάρχουν δύο γειτονικές περιοχές με τα ίδια χρώματα.

---

Δύο περιοχές ονομάζονται γειτονικές αν έχουν ένα κοινό σύνορο, χωρίς να σχηματίζουν κορυφή, καθώς οι κορυφές αποτελούν σημεία που είναι κοινά για τρεις ή περισσότερες περιοχές.

Για παράδειγμα, στο χάρτη των Ηνωμένων Πολιτειών της Αμερικής, η Γιούτα και η Αριζόνα είναι γειτονικές πολιτείες, αλλά η Γιούτα και το Νέο Μεξικό, οι οποίες έχουν μόνο ένα κοινό σημείο το οποίο ανήκει επίσης στην Αριζόνα και το Κολοράντο, δεν είναι.

Πως δημιουργήθηκε το πρόβλημα των τεσσάρων χρωμάτων

Στις 23 Οκτώβριου  του 1852, ο Φράνσις Γκάθρι (Francis Guthrie) , προπτυχιακός φοιτητής  στο University College του Λονδίνου όταν προσπάθησε να χρωματίσει τον χάρτη των περιφερειών της Αγγλίας  αναρωτήθηκε ποιος θα ήταν ο ελάχιστος αριθμός διαφορετικών χρωμάτων τα οποία θα χρησιμοποιούσε ώστε οι γειτονικές περιφέρειες να έχουν διαφορετικό χρώμα. Δεν κατέληξε πουθενά  όποτε  έθεσε στον καθηγητή Αύγουστο  Ντε Μόργκαν (Augustus De Morgan) το ερώτημα. Ο Ντε Μόργκαν ήταν ο πρώτος καθηγητής μαθηματικών του νεοσύστατου πανεπιστήμιου University College και διάσημος για τις έρευνες του πάνω στην Λογική.

Όμως παρά την εξαιρετική του ευφυΐα, ο Ντε Μοργκαν δεν ήξερε την απάντηση στην ερώτηση του μαθητή του. Την ίδια μέρα έγραψε στον συνάδελφο του Χαμιλτον,  «τον εξυπνότερο άνθρωπο της Ιρλανδίας», στο Δουβλίνο:

«Ένας μαθητής μου με ρώτησε σήμερα να του αιτιολογήσω ένα γεγονός το όποιο αγνοούσα – και εξακολουθώ να αγνοώ – αν είναι γεγονός. Λέει ότι αν ένα σχήμα είναι χωρισμένο σε τμήματα με οποιοδήποτε τρόπο και κάθε τμήμα είναι χρωματισμένο ώστε να έχει διαφορετικό χρώμα από οποιοδήποτε άλλο με το οποίο συνορεύει-μπορεί να απαιτούνται τέσσερα χρώματα, αλλά όχι παραπάνω… Αν μου δώσεις κάποια πολύ απλή εξήγηση που θα με κάνει να νιώσω  ένα αδαές ζώο, μάλλον θα ακολουθήσω το παράδειγμα της σφίγγας ….»
Ο Ντε Μοργκαν αναφερόταν στην μυθολογική σφίγγα η  οποία αυτοκτόνησε αφού ο Οιδίποδας  έλυσε τον γρίφο της. Βεβαίως ήταν μάλλον αρκετά πιο εύκολος από την εικασία των τεσσάρων χρωμάτων:
«Ποιο ζώο περπατά με τέσσερα πόδια  το πρωί, δυο το μεσημέρι και τρία το απόγευμα;» Η απάντηση  είναι άνθρωπος (αν η μέρα αντιστοιχεί στην ζωή του ανθρώπου , ως βρέφος μπουσουλάγε , ως ενήλικος περπατά με τα δυο πόδια και ως ηλικιωμένος με μπαστούνι).

Ούτε  όμως ο Χάμιλτον γνώριζε την απάντηση και μέσα σε τρεις μέρες του έγραψε: «Δεν νομίζω να ασχοληθώ σύντομα με την τετράδα των χρωμάτων σου.»

Πολλοί μαθηματικοί μεγάλου βεληνεκούς δοκίμασαν την τύχη τους με το πρόβλημα, μάταια όμως. Χαρακτηριστικό παράδειγμα ο καλύτερος φίλος του Χιλμπερτ στο Γκετιγκεν, ο Χέρμαν Μινκοφσκι . Όταν το ερώτημα τέθηκε σε κάποιο από τα μαθήματα του, σχολίασε:
«Το θεώρημα δεν έχει ακόμα αποδειχτεί, αλλά αυτό οφείλεται στο ότι ασχολήθηκαν μαζί του μόνο μαθηματικοί τρίτης κατηγορίας». «Πιστεύω ότι μπορώ να το αποδείξω!!» Αφιέρωσε  αρκετά μαθήματα, παλεύοντας με διαφορές ιδέες  στον πίνακα. Τέλος, κάποιο πρωί, μπαίνοντας στην τάξη, έσκασε η βόμβα: «Οι ουρανοί εξοργίστηκαν από την αλαζονεία μου», ομολόγησε: «Η απόδειξη μου είναι ελαττωματική!»

Το τοπολογικό αυτό πρόβλημα  έγινε γνωστό ως το πρόβλημα των τεσσάρων χρωμάτων  του χάρτη και το ερώτημα που έθεσε ο Φράνσις Γκάθρι έμεινε γνωστό ως το θεώρημα των τεσσάρων χρωμάτων. Μπορούμε να δούμε την πιο συνήθη περίπτωση του ανοίγοντας έναν πολιτικό χάρτη. Οι διαφορετικές χώρες  που εικονίζονται πρέπει να χρωματιστούν διαφορετικά ώστε να ξεχωρίζουν εύκολα.

Πηγή: http://mathhmagic.blogspot.com/2011/03/blog-post_16.html